
Какво прави пресечната точка на медианите? Основни елементи на триъгълник abc. Приложение на медианите в математическата статистика
Урок 1
Медиани на триъгълник. Пресечна точка на медианите.
Медиана на триъгълник е отсечката, свързваща върха на триъгълника със средата на срещуположната страна.
Доказателство:
Пресечната точка на медианите на триъгълник е център на тежестта този триъгълник.
Проблем 1Пресечната точка на медианите на триъгълник е отделена от върховете му на разстояния, равни на 4, 6 и 8. Намерете дължините на медианите на триъгълника.
Решение.Нека AM, BE и CD са медианите в триъгълник ABC, K е тяхната пресечна точка, KS=4, KA=6 и KB=8.
https://pandia.ru/text/78/182/images/image004_34.gif" width="76" height="50">, тоест има 2 части на сегмент KA и една част на сегмент KM, тогава цялата медиана AM се състои от три равни частии https://pandia.ru/text/78/182/images/image006_24.gif" width="104" height="41">.
по същия начин,
![]() ,
, ![]()
Отговор: 6, 9 и 12
Проблем 2Медианите AM и SC на триъгълник ABC са взаимно перпендикулярни и равни съответно на 6 и 9. Изчислете дължините на страните AB и BC.
https://pandia.ru/text/78/182/images/image010_15.gif" width="104" height="41">,
Ето защо ![]() И
И
![]() ,
, ![]() .
.
Освен това
![]() ,
, ![]() .
.
Използвайки теоремата на Питагор, изчисляваме дължините на сегментите AK и SM, получаваме
Сега нека изчислим дължините на страните AB и BC:
AB=2AK=10, BC=2CM=.
Отговор: 10;.
Тест за самоконтрол.
1. Медианата на триъгълник се дели наполовина (изберете един от отговорите)
1) ъгъл на триъгълник
2) страна на триъгълника
3) две страни на триъгълника
2. В какво съотношение разделя пресечната точка на медианите на триъгълник всяка от медианите на триъгълника (изберете верния отговор).
1) 2:1, броено от основата на триъгълника
2) 1:2, считано от върха на триъгълника
3) 2:1, считано от върха на триъгълника
4) 1:2, като се брои от основата на триъгълника
5) на две равни части
3. Ако в триъгълник ABC са начертани медианата AM и P – пресечната точка на медианите на триъгълника, то каква част от медианата AM е отсечката AP? (изберете един от вариантите за отговор)
4. В триъгълник ABC са начертани медианата AM и P – пресечната точка на медианите на триъгълника. Каква част от медианата AM е сегментът PM? (изберете един от вариантите за отговор)
5. В триъгълник ABC са начертани медианата AM и P – пресечната точка на медианите на триъгълника. Каква част от сегмент AP е сегмент PM? (изберете един от вариантите за отговор)
Вижте верните отговори.
Задачи за самостоятелно решаване.
1. Пресечната точка на медианите на триъгълник се намира на разстояния равни на 6 cm, 8 cm и 12 cm от върховете му. Намерете дължините на медианите на триъгълника.
Вижте решението.
2. Медианите BM и SC на триъгълник ABC са взаимно перпендикулярни и равни съответно на 15 и 36. Намерете дължините на страните AB и AC.
Вижте решението.
3. Медианите на триъгълника са 6, 9 и 12. На какво разстояние от върховете е пресечната точка на медианите на триъгълника?
Вижте решението.
4. Медианите на триъгълника са 9, 12 и 18. Намерете разстоянията от средите на страните на триъгълника до центъра на тежестта даден триъгълник.
Вижте решението.
5. Центърът на тежестта на триъгълника е отдалечен от средите на страните му. Равно на 5, 6 и 7. Намерете медианите на този триъгълник.
Вижте решението.
6. Пресечната точка на медианите на триъгълник се отдалечава от средите на страните му на разстояния, равни на 2, 3 и 4. На какви разстояния от върховете на триъгълника се намира тази точка?
Вижте решението.
Гомел научно-практическа конференцияученици по математика, нейните приложения и информационни технологии"Търсене"
Резюме по темата:
"Медиани на триъгълник"
Ученици:
9" държавен клас
образователни институции
„Град Гомель
Многопрофилна гимназия №14"
Морозова Елизавета
Ходосовская Алеся
Научен съветник-
Учител по математика най-висока категория
Сафонова Алла Викторовна
Гомел 2009 г
Въведение
1. Медиани на триъгълник и техните свойства
2. Откритие на немския математик Г. Лайбниц
3. Прилагане на медиани в математическа статистика
4. Медиани на тетраедър
5. Шест доказателства на теоремата за медианата
Заключение
Списък на използваните източници и литература
Приложение
Въведение
Геометрията започва с триъгълник. Вече две хилядолетия триъгълникът е символ на геометрията, но не е символ. Триъгълникът е атом на геометрията.
Триъгълникът е неизчерпаем – непрекъснато се откриват нови негови свойства. За да разкажете за всичките му известни свойства, имате нужда от обем, сравним по обем с обема Голяма енциклопедия. Искаме да говорим за медианата на триъгълник и нейните свойства, както и за използването на медиани.
Първо, не забравяйте, че медианата на триъгълник е сегмент, свързващ върховете на триъгълника със средата на противоположната страна. Медианите имат много свойства. Но ние ще разгледаме едно свойство и 6 различни доказателства за него. Трите медиани се пресичат в една точка, която се нарича центроид (център на масата) и се разделят в съотношение 2:1.
Има медиани не само на триъгълник, но и на тетраедър. Сегментът, свързващ върха на тетраедъра с центроида (точката на пресичане на медианите) на противоположното лице, се нарича медиана на тетраедъра. Ще разгледаме и свойството на медианите на тетраедър.
Медианите се използват в математическата статистика. Например, за да намерите средната стойност на определен набор от числа.
1. Медиани на триъгълник и техните свойства
Както знаете, медианите на триъгълника са сегментите, свързващи неговите върхове със средните точки на противоположните страни. И трите медиани се пресичат в една точка и я разделят в съотношение 1:2.
Пресечната точка на медианите е и центърът на тежестта на триъгълника. Ако окачите картонен триъгълник в пресечната точка на неговите медиани, той ще бъде в състояние на равновесие
Любопитно е, че всичките шест триъгълника, на които всеки триъгълник е разделен от своите медиани, имат еднакви площи.
Медианите на триъгълник през неговите страни се изразяват, както следва:
, , .Ако две медиани са перпендикулярни, тогава сумата от квадратите на страните, на които те са пропуснати, е 5 пъти квадрата на третата страна.
Нека построим триъгълник, чиито страни са равни на медианите на дадения триъгълник, тогава медианите на построения триъгълник ще бъдат равни на 3/4 от страните на първоначалния триъгълник.
Нека наречем този триъгълник първи, триъгълника от неговите медиани - втори, триъгълника от медианите на втория - трети и т.н. Тогава триъгълниците с нечетни числа (1,3, 5, 7,...) са подобни един към друг и триъгълници с четни числа (2, 4, 6, 8,...) също са подобни един на друг.
Сборът от квадратите на дължините на всички медиани на триъгълник е равен на ¾ сбора от квадратите на дължините на неговите страни.
2. Откритие на немския математик Г. Лайбниц
Известен немски математик Г. Лайбниц откри забележителен факт: сумата от квадратите на разстоянията от произволна точка в равнината до върховете на триъгълник, лежащ в тази равнина, е равна на сумата от квадратите на разстоянията от точката на пресичане на медианите до неговите върхове, добавени за утрояване на квадрата на разстоянието от точката на пресичане на медианите до избраната точка.
От тази теорема следва, че точката на равнината, за която сумата от квадратите на разстоянията до върховете на даден триъгълник е минимална, е пресечната точка на медианите на този триъгълник.
В същото време минималната сума от разстояния до върховете на триъгълника (а не техните квадрати) ще бъде за точката, от която всяка страна на триъгълника се вижда под ъгъл от 120 °, ако нито един от ъглите на триъгълник е по-голям от 120° (точка на Ферма), а за върха тъп ъгъл, ако е по-голям от 120°.
От теоремата на Лайбниц и предишното твърдение е лесно да се намери разстоянието дот точката на пресичане на медианите до центъра на описаната окръжност. Всъщност, според теоремата на Лайбниц, това разстояние е равно на квадратен корен от една трета от разликата между сумата от квадратите на разстоянията от центъра на описаната окръжност до върховете на триъгълника и сумата
Квадрати на разстоянията от пресечната точка на медианите до върховете на триъгълника. Разбираме това
.Точка Мпресечната точка на медианите на триъгълника ABC е единствената точка от триъгълника, за която сумата от векторите MA,М.Б.и MSравно на нула. Координати на точки М(спрямо произволни оси) са равни на средните аритметични стойности на съответните координати на върховете на триъгълника. От тези твърдения можем да получим доказателство на теоремата за медианата.
3. Приложение на медианите в математическата статистика
Медианите съществуват не само в геометрията, но и в математическата статистика. Да предположим, че трябва да намерим средната стойност на определен набор от числа
, , ..., a p.Можете, разбира се, да приемете средната аритметична стойност като средна стойностНо понякога е неудобно. Да кажем, че трябва да определим средния ръст на второкласниците в Москва. Нека да интервюираме 100 ученици на случаен принцип и да запишем ръста им. Ако едно от момчетата шеговито каже, че височината му е километър, тогава средната аритметична стойност на написаните числа ще се окаже твърде голяма. Много по-добре е да се вземе като средно Медианачисла
, ..., a p.Да приемем, че има нечетен брой числа и да ги подредим в ненамаляващ ред. Числото в средата се нарича медиана на множеството. Например медианата на набора от числа 1, 2, 5, 30, 1, 1, 2 е 2 (а средноаритметичното е много по-голямо – то е 6).
4. Медиани на тетраедър
Оказва се, че можем да говорим за медиани не само за триъгълник, но и за тетраедър. Сегментът, свързващ върха на тетраедъра с центроида (точката на пресичане на медианите) на противоположното лице, се нарича Медианатетраедър. Подобно на медианите на триъгълника, медианите на тетраедъра се пресичат в една точка, центъра на масата или центроида на тетраедъра, но съотношението, в което се разделят в тази точка, е различно - 3:1, броено от върховете. Една и съща точка лежи на всички сегменти, свързващи средните точки на противоположните ръбове на тетраедъра, неговите бимедиани, и ги разделя наполовина. Това може да се докаже, например, от механични съображения чрез поставяне на тежести с единица маса на всеки от четирите върха на тетраедъра.
5. Шест доказателства на теоремата за медианата
Отдавна е отбелязано, че е по-полезно да се запознаете с различни решения на един проблем, отколкото с подобни решения на различни проблеми. Една от теоремите, която, подобно на много други класически теореми на елементарната геометрия, допуска няколко поучителни доказателства, е
Теорема за медианите на триъгълник. Медиани, B и C на триъгълникABCсе пресичат в някаква точка M и всяка от тях е разделена от тази точка по отношение 2:1, броейки отгоре:А.М.: М= Б.М.: М= СМ.: М=2. (1)
Във всички доказателства, дадени по-долу, с изключение на шестото, установяваме само това медиана B минава през точка M, която разделя медиана A в отношение 2:1. Ако в съответния аргумент заместим сегмента INза сегмент С ,тогава разбираме това СЪСпреминава през М.Това ще докаже, че и трите медиани се пресичат в дадена точка М,и AM:M - 2.Тъй като всички медиани са равни, можем да заменим АНа INили SS 1оттук следва (1).
Медианата е една от основните линии на триъгълника. Този сегмент и правата линия, на която той лежи, свързват точката в началото на ъгъла на триъгълника със средата на срещуположната страна на същата фигура. В равностранен триъгълник медианата също е ъглополовяща и надморска височина.Свойството на медианата, което значително ще улесни решаването на много задачи, е следното: ако нарисувате медиани от всеки ъгъл в триъгълник, тогава всички те, пресичащи се в една точка, ще бъдат разделени в съотношение 2: 1. Съотношението трябва да се брои от върха на ъгъла.
Медианата има тенденция да разделя всичко по равно. Например всяка медиана разделя триъгълник на два други равни по площ. И ако нарисувате и трите медиани, тогава в голям триъгълник ще получите 6 малки, също равни по площ. Такива фигури (с еднаква площ) се наричат равни по площ.
Симетрала
Симетрала е лъч, който започва от върха на ъгъл и разполовява същия ъгъл. Точките, лежащи на даден лъч, са на еднакво разстояние от страните на ъгъла. Свойствата на ъглополовящата са полезни при решаването на проблеми, включващи триъгълници.В триъгълник ъглополовяща е сегмент, който лежи върху ъглополовящия лъч на ъгъла и свързва върха с противоположната страна. Точката на пресичане със страна я разделя на сегменти, чието съотношение е равно на съотношението на страните, съседни на тях.
Ако окръжност е вписана в триъгълник, тогава нейният център ще съвпада с пресечната точка на всички ъглополовящи на дадения триъгълник. Това свойство е отразено и в стереометрията - там ролята на триъгълник играе пирамида, а ролята на кръг - топка.
Височина
Точно като медианата и ъглополовящата, надморската височина в триъгълник основно свързва върха на ъгъла и противоположната страна. Тази връзка произтича от следното: височината е перпендикуляр, начертан от връх към права линия, която съдържа противоположната страна.Ако надморска височина е начертана в правоъгълен триъгълник, тогава, докосвайки противоположната страна, тя разделя целия триъгълник на два други, които от своя страна са подобни на първия.
Концепцията за перпендикуляр често се използва в стереометрията за определяне на относителните позиции на прави линии в различни равнини и разстоянието между тях. В този случай сегментът, който изпълнява функцията на перпендикуляр, трябва да има прав ъгъл с двете прави линии. Тогава числова стойностна този сегмент ще покаже разстоянието между две фигури.
Урок 3
Медианата разделя площта на триъгълника наполовина
Два триъгълника се наричат равни по размер. Ако имат еднаква площ.
Теорема 1.Медианата разделя триъгълник на два равни триъгълника.
Доказателство:
Нека BM е медианата на триъгълник ABC. Нека докажем това
https://pandia.ru/text/78/448/images/image002_97.jpg" width="289" height="227">
Нека намерим надморската височина BH на триъгълник ABC. Тогава
 ,
,
https://pandia.ru/text/78/448/images/image005_99.gif" width="136" height="34 src=">.
https://pandia.ru/text/78/448/images/image007_80.gif" width="217" height="55 src=">.
Q.E.D.
Теорема 2. Медианите на триъгълник го разделят на шест равни триъгълника.


От теоремата, по-специално, следва, че ако точката на пресичане на медианите на триъгълник е свързана с всичките му върхове, тогава триъгълникът ще бъде разделен на триравни части.
Проблем 1 Двете медиани на триъгълника са взаимно перпендикулярни и съответно равни на 3 и 4. Намерете площта на триъгълника.
Решение.
Нека в триъгълник ABC медианите AM и BE са равни съответно на 3 и 4, , K е пресечната точка на медианите.

https://pandia.ru/text/78/448/images/image013_46.gif" width="120" height="47 src=">.
Тъй като триъгълник ABC е прав ъгъл с прав ъгъл BKA, тогава ![]() .
.
Тъй като медианите разделят триъгълник на 6 равни части, тогава .
Отговор: 8
Проблем 2 Медианите на триъгълника са 6, 8 и 10, намерете площта на триъгълника.

Решение.
Нека медианите АМ, БЪДАИ CDна даден триъгълник са съответно 6, 8 и 10, K е пресечната им точка. Върху продължението на лъч BE отвъд точка E да начертаем отсечка EF= KE. Нека свържем точки C, F и A.
Помислете за триъгълник KAF.
https://pandia.ru/text/78/448/images/image018_31.gif" width="152" height="41 src=">
https://pandia.ru/text/78/448/images/image020_25.gif" width="67" height="19 src=">, тъй като CKAE е успоредник (въз основа на успоредника: ако диагоналите на четириъгълник са разделени от точката на пресичане наполовина, към даден четириъгълен успоредник), получаваме ![]() .
.
Тъй като https://pandia.ru/text/78/448/images/image023_26.gif" width="125" height="20 src=">, тогава според обратна на теорематаПитагор (ако квадратът на едната страна на триъгълника равно на суматаквадрати на другите му две страни, тогава триъгълникът е правоъгълен) триъгълник KAF е правоъгълен и.
Нека изчислим площта на триъгълника AKF:
https://pandia.ru/text/78/448/images/image026_24.gif" width="104" height="41 src=">.gif" width="104" height="41 src=">.
https://pandia.ru/text/78/448/images/image030_18.gif" width="16 height=41" height="41"> от площта на самия триъгълник.
Доказателството може да се види например в методическо ръководство"Основни проблеми на планиметрията."
Въпроси за самопроверка:
1. Какви триъгълници се наричат равноповърхни?
2. Площта на триъгълника е равна на S. Каква е площта на всеки от триъгълниците, на които е разделен от медианата, начертана към всяка страна на този триъгълник?
3. На колко равни части разделя триъгълника трите начертани в него медиани?
4. Площта на триъгълника е S. Центърът на тежестта на този триъгълник е свързан с неговите върхове. Каква е площта на всеки от получените триъгълници?
5. Площта на триъгълника е 48, каква е площта на триъгълника, съставен от медианите на този триъгълник?
6. Площта на триъгълник, съставен от медианите на триъгълник, е 24, каква е площта на триъгълника?
Вижте отговорите.
Задачи за самостоятелно решаване:
1. Две медиани на триъгълник са взаимно перпендикулярни и равни съответно на 6 и 8. Намерете площта на триъгълника.
Вижте решението.
2. Медианите на триъгълника са 3, 4 и 5, намерете площта на триъгълника.
Вижте решението.
3. Триъгълник ABC, чиито страни са 13 cm, 14 cm и 15 cm, е разделен на три триъгълника с отсечки, свързващи точката Мпресичане на медианите на триъгълник с върховете на триъгълник. Намерете площта на триъгълник ВМС.
Вижте решението.
4. Двете страни на триъгълник са равни на 10 и 12, а медианата, прекарана към третата, е равна на 5. Намерете площта на триъгълника.
Вижте решението.
При решаването на геометрични задачи е полезно да следвате такъв алгоритъм. Докато четете условията на проблема, е необходимо
- Направете рисунка. Чертежът трябва да съответства възможно най-много на условията на проблема, така че основната му задача е да помогне да се намери решението
- Поставете всички данни от постановката на задачата върху чертежа
- Запишете всички геометрични понятия, които се появяват в проблема
- Запомнете всички теореми, които се отнасят до тези концепции
- Начертайте върху чертежа всички връзки между елементите геометрична фигура, които следват от тези теореми
Например, ако думата ъглополовяща на ъгъл на триъгълник се появи в задача, трябва да запомните дефиницията и свойствата на ъглополовяща и да посочите равно или пропорционални сегментии ъгли.
В тази статия ще намерите основните свойства на триъгълник, които трябва да знаете успешно решениезадачи.
ТРИЪГЪЛНИК.
Площ на триъгълник.
1. ,
тук - произволна страна на триъгълника, - височината, спусната до тази страна.

2.
 ,
,
тук и са произволни страни на триъгълника, и е ъгълът между тези страни:

3. Формула на Херон:

Това са дължините на страните на триъгълника, това е полупериметърът на триъгълника,
4. ,
тук е полупериметърът на триъгълника и е радиусът на вписаната окръжност.

Нека са дължините на допирателните сегменти.

Тогава формулата на Heron може да бъде записана по следния начин:
5.

6. ,
тук - дължините на страните на триъгълника, - радиусът на описаната окръжност.

Ако се вземе точка от страната на триъгълник, която разделя тази страна в съотношение m: n, тогава сегментът, свързващ тази точка с върха на противоположния ъгъл, разделя триъгълника на два триъгълника, чиито площи са в отношение м: н:

Отношението на площите на подобни триъгълници е равно на квадрата на коефициента на подобие.
Медиана на триъгълник
Това е сегмент, свързващ върха на триъгълник със средата на противоположната страна.

Медиани на триъгълниксе пресичат в една точка и се разделят от пресечната точка в съотношение 2:1, като се брои от върха.

Пресечната точка на медианите на правилен триъгълник разделя медианата на два сегмента, по-малкият от които е равен на радиуса на вписаната окръжност, а по-големият е равен на радиуса на описаната окръжност.
 Радиусът на описаната окръжност е два пъти радиуса на вписаната окръжност: R=2r
Радиусът на описаната окръжност е два пъти радиуса на вписаната окръжност: R=2r
Средна дължинапроизволен триъгълник
 ,
,
тук - медианата, изтеглена към страната - дължините на страните на триъгълника.
Симетрала на триъгълник
Това е ъглополовящата на всеки ъгъл на триъгълник, свързващ върха на този ъгъл с противоположната страна.

Симетрала на триъгълникразделя страна на сегменти, пропорционални на съседните страни:

Симетрали на триъгълниксе пресичат в една точка, която е центърът на вписаната окръжност.

Всички точки на ъглополовящата са на еднакво разстояние от страните на ъгъла.

Височина на триъгълник
Това е перпендикулярен сегмент, спуснат от върха на триъгълника до противоположната страна, или нейното продължение. В тъп триъгълник надморската височина, изтеглена от върха на острия ъгъл, е извън триъгълника.

Височините на триъгълник се пресичат в една точка, която се нарича ортоцентър на триъгълника.
Да се намери височината на триъгълникизтеглен отстрани, трябва да намерите неговата площ по всеки наличен начин и след това да използвате формулата:
Център на описаната окръжност на триъгълник, лежи в пресечната точка на ъглополовящите, прекарани към страните на триъгълника.

Радиус на обиколката на триъгълник може да се намери с помощта на следните формули:
Ето дължините на страните на триъгълника и е площта на триъгълника.
 ,
,
където е дължината на страната на триъгълника и е срещуположният ъгъл. (Тази формула следва от синусовата теорема.)
Неравенство на триъгълник
Всяка страна на триъгълника е по-малка от сбора и по-голяма от разликата на другите две.
Сумата от дължините на всеки две страни винаги е по-голяма от дължината на третата страна:
Срещу по-голямата страна лежи по-големият ъгъл; Срещу по-големия ъгъл лежи по-голямата страна:
Ако , то обратното.
Теорема за синусите:
Страните на триъгълника са пропорционални на синусите на противоположните ъгли:


Косинусова теорема:
Квадратът на една страна на триъгълник е равен на сбора от квадратите на другите две страни без удвоеното произведение на тези страни по косинуса на ъгъла между тях:
![]()
Правоъгълен триъгълник
- Това е триъгълник, чийто един от ъглите е 90°.
Сума остри ъглина правоъгълен триъгълник е 90°.
Хипотенузата е страната, която лежи срещу ъгъла от 90°. Хипотенузата е най-дългата страна.
Питагорова теорема:
квадратът на хипотенузата е равен на сумата от квадратите на катетите: ![]()

Радиусът на окръжност, вписана в правоъгълен триъгълник, е равен на
 ,
,
тук е радиусът на вписаната окръжност, - краката, - хипотенузата:
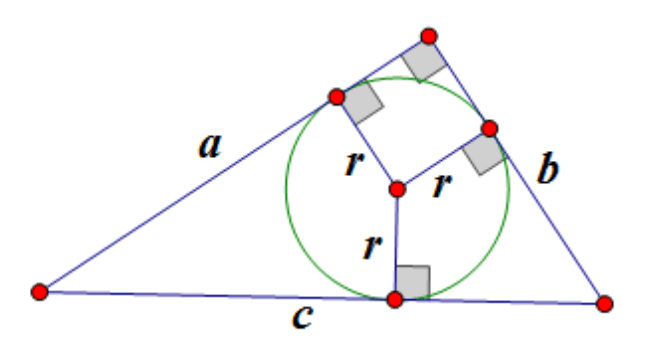
Център на описаната окръжност на правоъгълен триъгълник лежи в средата на хипотенузата:
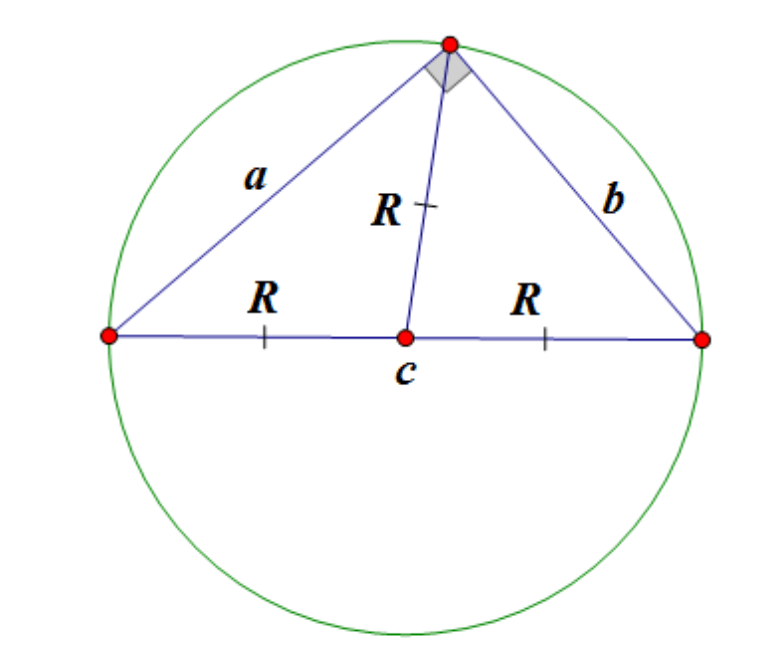
Медиана на правоъгълен триъгълник, начертана към хипотенузата, е равно на половината от хипотенузата.
Дефиниция на синус, косинус, тангенс и котангенс на правоъгълен триъгълниквиж
Съотношението на елементите в правоъгълен триъгълник:
Квадрат на надморската височина на правоъгълен триъгълник, изтеглен от връх прав ъгъл, е равно на произведението на проекциите на краката върху хипотенузата:
![]()
Квадратът на крака е равен на произведението на хипотенузата и проекцията на крака върху хипотенузата:

Крак, лежащ срещу ъгъла равно на половината от хипотенузата:

![]()
Равнобедрен триъгълник.
Симетрала равнобедрен триъгълник, начертана към основата е медианата и височината.
В равнобедрен триъгълник ъглите при основата са равни.

Върхов ъгъл.
И - страни,
И - ъгли в основата.
Височина, ъглополовяща и медиана.
внимание!Височината, ъглополовящата и медианата, прекарани отстрани, не съвпадат.
Правилен триъгълник
(или равностранен триъгълник ) е триъгълник, всички страни и ъгли на който са равни.

Площ на правилен триъгълникравна на
където е дължината на страната на триъгълника.
Център на окръжност, вписана в правилен триъгълник, съвпада с центъра на окръжността, описана около правилен триъгълник и се намира в пресечната точка на медианите.
Пресечна точка на медианите на правилен триъгълникразделя медианата на два сегмента, по-малкият от които е равен на радиуса на вписаната окръжност, а по-големият е равен на радиуса на описаната окръжност.
Ако един от ъглите на равнобедрен триъгълник е 60°, то триъгълникът е правилен.
Средна линия на триъгълника
Това е сегмент, свързващ средните точки на двете страни.
На фигурата DE е средната линия на триъгълник ABC.
Средната линия на триъгълника е успоредна на третата страна и равна на нейната половина: DE||AC, AC=2DE

Външен ъгъл на триъгълник
Това е ъгълът, съседен на всеки ъгъл на триъгълника.
Външен ъгъл на триъгълник е равен на сбора от два ъгъла, които не са съседни на него.

Тригонометрични функции на външен ъгъл:
Признаци за равенство на триъгълници:
1 . Ако две страни и ъгълът между тях на един триъгълник са съответно равни на две страни и ъгълът между тях на друг триъгълник, тогава тези триъгълници са еднакви.

2 . Ако страна и два съседни ъгъла на един триъгълник са съответно равни на страна и два съседни ъгъла на друг триъгълник, тогава тези триъгълници са еднакви.

3 Ако три страни на един триъгълник са съответно равни на три страни на друг триъгълник, тогава тези триъгълници са еднакви.

Важно:тъй като в правоъгълен триъгълник два ъгъла са очевидно равни, тогава за равенство на две правоъгълни триъгълници изисква се равенство само на два елемента: две страни или страна и остър ъгъл.
Признаци за сходство на триъгълници:
1 . Ако две страни на един триъгълник са пропорционални на две страни на друг триъгълник и ъглите между тези страни са равни, тогава тези триъгълници са подобни.
2 . Ако три страни на един триъгълник са пропорционални на три страни на друг триъгълник, тогава триъгълниците са подобни.
3 . Ако два ъгъла на един триъгълник са равни на два ъгъла на друг триъгълник, тогава триъгълниците са подобни.
Важно:В подобни триъгълници подобни страни лежат срещу равни ъгли.
Теорема на Менелай
Нека линия пресича триъгълник и е точката на пресичане със страната , е точката на пресичане със страната и е точката на пресичане с продължението на страната . Тогава
